- An edge is a place of rapid change in the image intensity function (or grey-level function), which manifests as boundaries between physically distinct regions.
- i.e. a peak in the derivative of the image function
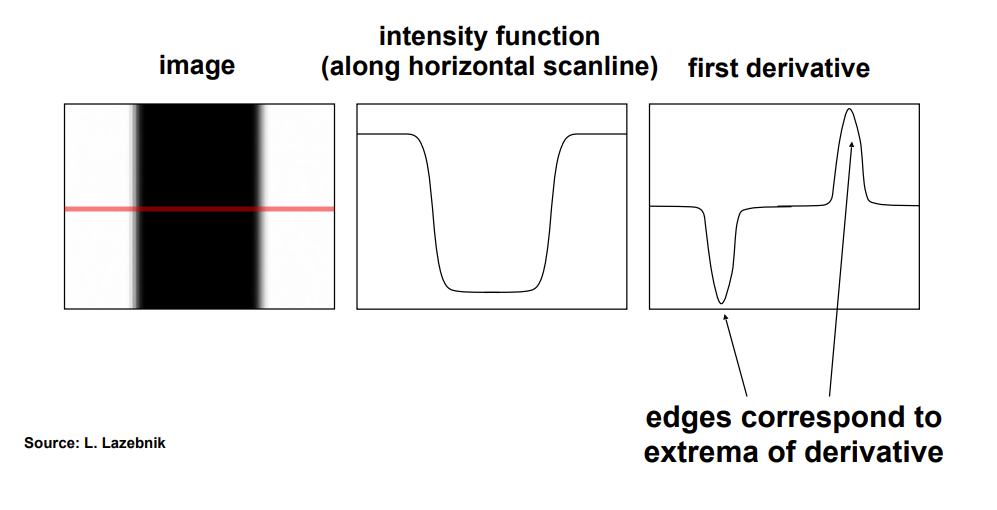
- i.e. a peak in the derivative of the image function
Convolution based Edge Detection>
see Convolution
- Edge detection is same as differentiation a.k.a. derivative filter
- -

- gradient direction is perpendicular to the edge
Derivative of Gaussian convolution kernel
- For noisy images -
- scale selection is important
- edges may be noise
- Location of edges at coarse scale can direct the search for finer-scale edges
- edges can persist across scales, allows fusion across scales
- Perform Image smoothing before derivative filter to reduce effect of noise
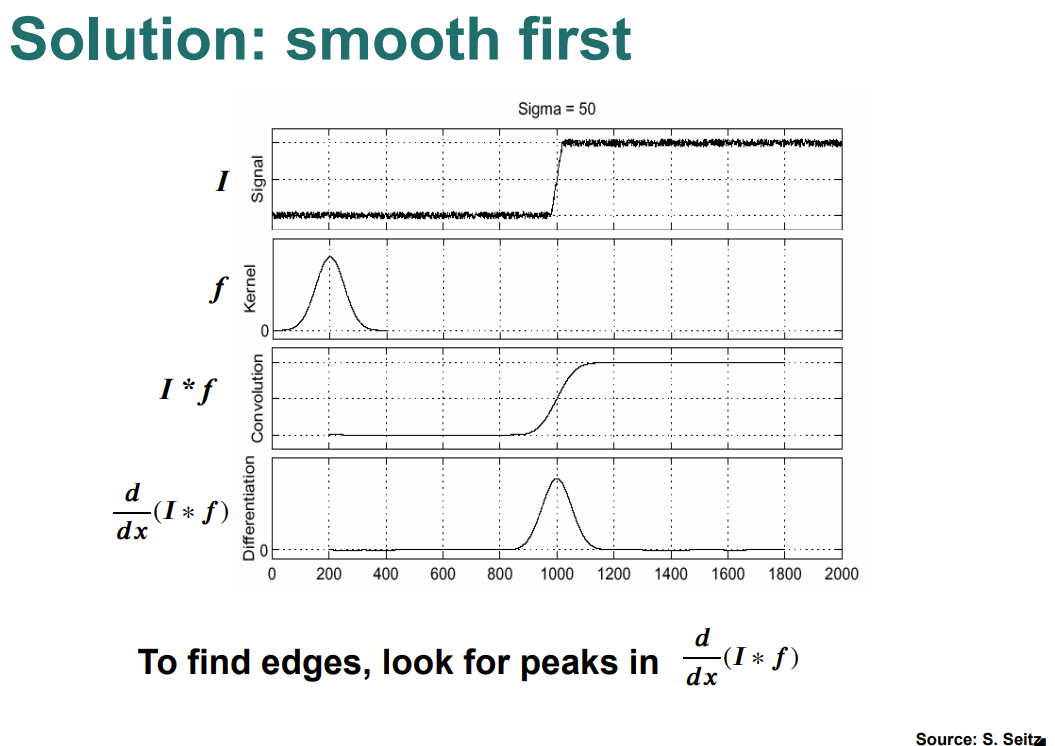
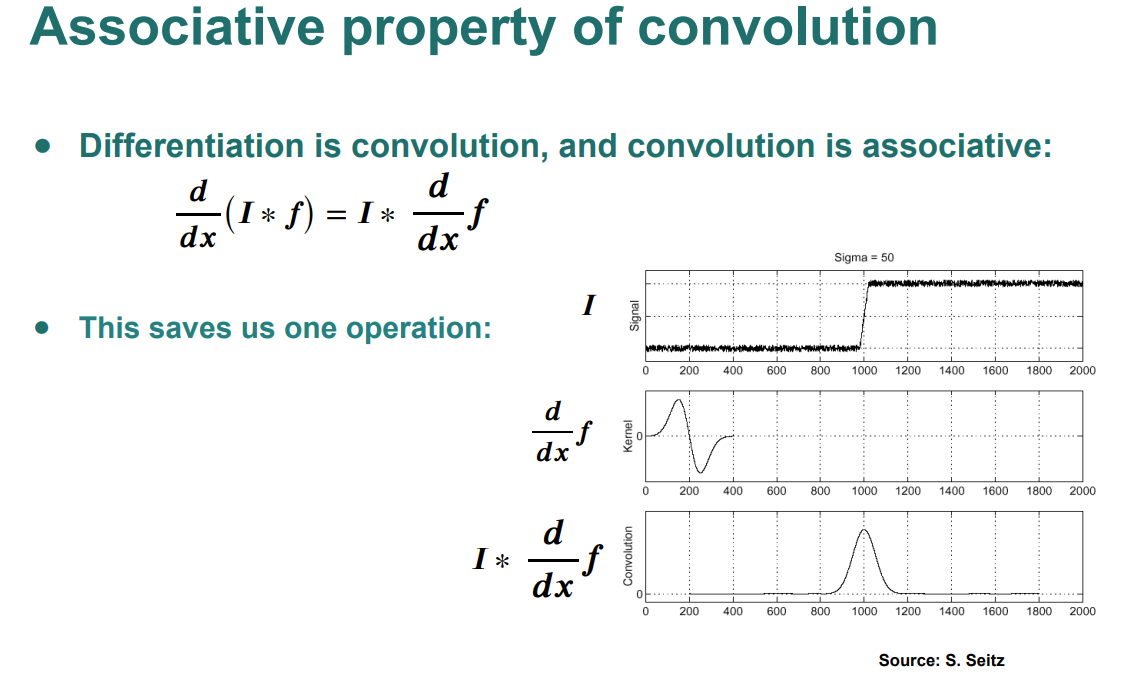
- scale selection is important
- Derivative of Gaussian filter in 2 dimensions, along x
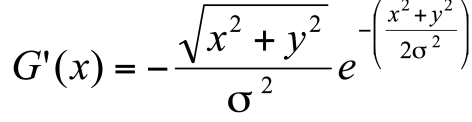
- derivatives can be along x and y directions (2 filters) → requires atleast 2 convolutions
- allows selection of scale of edge detection
- through σ
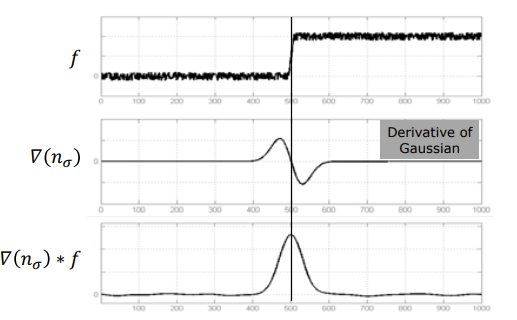
- through σ
Kernels
Prewitt Kernel
- vertical edges, detecting edges across x direction, smooths along y direction
- -1 0 1
- -1 0 1
- -1 0 1
- horizontal edges, detecting edges across y direction, smooths along x direction
- -1 -1 -1
- 0 0 0
- 1 1 1
Sobel Kernel
- vertical edges, detecting edges in x direction, weighted smoothing along y direction
- -1 0 1
- -2 0 2
- -1 0 1
- horizontal edges, detecting edges in y direction, weighted smoothing along x direction
- -1 -2 -1
- 0 0 0
- 1 2 1
- 2 filters: Derivative images I’x and I’ y

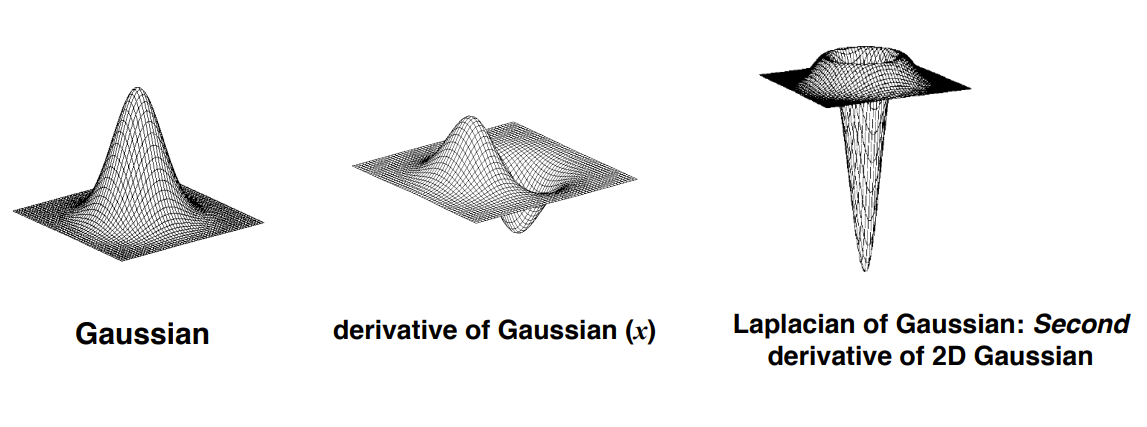
Laplacian of Gaussian Edge Detector
a.k.a. Marr–Hildreth Edge Detector a.k.a. Mexican hat wavelet
- second derivative of gaussian kernel
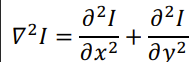
- 2nd Derivative of Gaussian filter in 2 dimensions
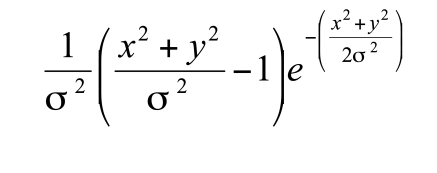
- detect zero crossings → where the 2nd derivative crosses zero → indicates an edge
- convolution kernel has a negative center and a positive surrounding
- again, scale selection is done through σ
- isotropic response
- one filter (all directions)
- no edge direction
- indirect edge magnitude
- one filter (all directions)
- kernel examples
2 -1 2
-1 -4 -1
2 -1 2
1 1 1
1 -8 1
1 1 1
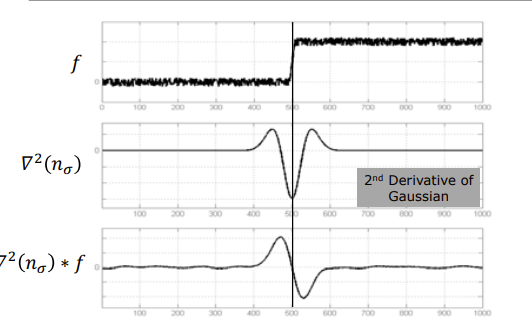
Canny Edge Detector
- best attributes of both the gradient operator and the Laplacian operator
- Multi stage algorithm
- Gaussian Smoothing to select scale and smoothen
- edge detection
- convolve image intensity function with derivative of Gaussian (Sobel operator)
- Edge magnitude and direction detected
- Compute Laplacian of Gaussian along the Gradient Direction at each pixel
- zero crossings → edge location
- less effected by pixels that are unrelated to the edge
- thinning: suppress non maxima of derivative
- non maxima derivatives across an edge
- sub pixel precision: detect precise edge locations
- Track using hysteresis thresholds
- Finalize the detection of edges by suppressing all the other edges that are weak and not connected to strong edges.
- declare each pixel as being an edge or not
- single threshold: if the edge magnitude is less than some value T it is not an edge

Difference of Gaussians Edge Detector
- a fast approximation of the Laplacian of Gaussians
- subtraction of one Gaussian-Blurred (Gaussian Smoothing) version of an image from another, less blurred image
- for scales of gaussians sσ and σ →
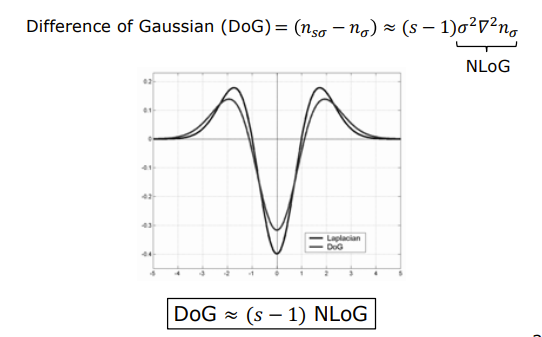
- DoG = (s-1) NLoG
Edge illusions
Cannot be detected using edge detectors
Herring Illusion
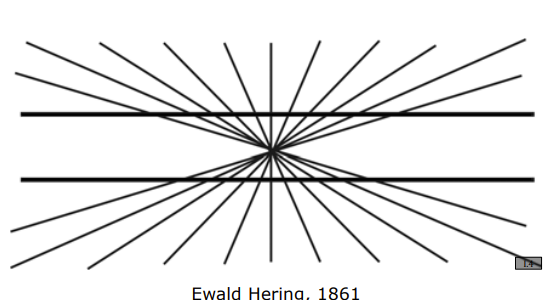 horizontal lines are actually parallel
horizontal lines are actually parallel
Cafe Wall Illusion
 horizontal lines are actually parallel
horizontal lines are actually parallel