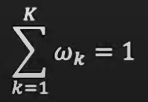a.k.a GMMs Probabilistic Clustering Model
- Clusters are the hills in the normalized density function of distribution of the feature space.
- The distribution of the feature space can have varying densities → more points in a space makes it more dense
- normalized density function → returns the density
- peak or mode of the hill is the cluster center.
- look at the density function as a probability distribution function
- fit a mixture of gaussian models is used to model this probability distribution
- can handle overlapping clusters → assigns points to clusters with some probability
- Generative, as it gives a probability model of x
- fitting 1 gaussian distribution to 1-dimensional gaussian-
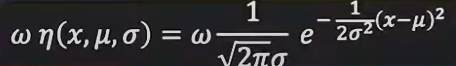
- where, ω is the scale or evidence
- μ is the mean and σ is the std dev of the gaussian η
High dimensional GMM
- Assume the probability distribution P(x) in some D-dimensions is made of k different gaussians
- weighted sum of k gaussians
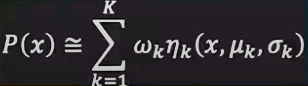
- such that
- where x ∈ RD
- X belongs to gaussian k for which
- ||X - μk|| is min and
- ||X - μk|| < 2.5σk - Equivalent Latent variable form
- p(z=k) = ωk
- select a mixture component with probability ω
- p(x | z = k) = η(x ; μk, σ k)
- sample from that component’s gaussian
- then p(x) is the marginal over x
- z is the latent variable
- p(z=k) = ωk
Expectation-Maximization (EM) Algorithm
- start with k clusters. Select some μc, σ c and ωc (a.k.a. πc ) for all the clusters.
- Expectation step:
- for all x datapoints, compute soft probabilities ric, the probability that xi belongs to cluster c →N x K matrix
- normalize to sum to one
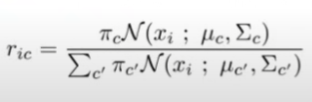
- if xi likely belongs to cluster c, πc for the cluster will be high
- Maximization step:
- fixing the ric, recompute the cluster parameters
- for each cluster

- Repeat E-M steps until convergence
- each step increases the log-likelihood P(x)
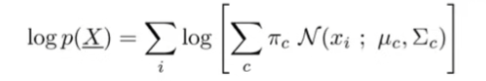
- convergence when log-likelihood doesn’t change much
- convergence guaranteed
How to choose k?
- penalize the log-likelihood scores
Pros
- can handle overlapping clusters
Cons
- sensitive to initialization parameters - can converge to local optima
- reinitialize multiple times
Alternatives
- Stochastic EM
- Hard EM